剑指 Offer 62. 圆圈中最后剩下的数字思路推导(约瑟夫环、DP、递归)
一、题目
剑指 Offer 41 数据流中的中位数
题目详细描述
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
1 | [2,3,4] 的中位数是 3 |
二、分析
详细分析
传统方法
求一个数据流的中位数,咋一看很简单。我们下意识的会想到直接用排序的方法,在每次查找中位数的时候,进行排序(快排,堆排,冒泡等皆可),利用中位数下标定位并返回中位数结果。但是这种方法对于频繁的求中位数,需频繁进行排序,时间复杂度太高,会超出时间限制。
堆堆求中位数方法
数据结构准备
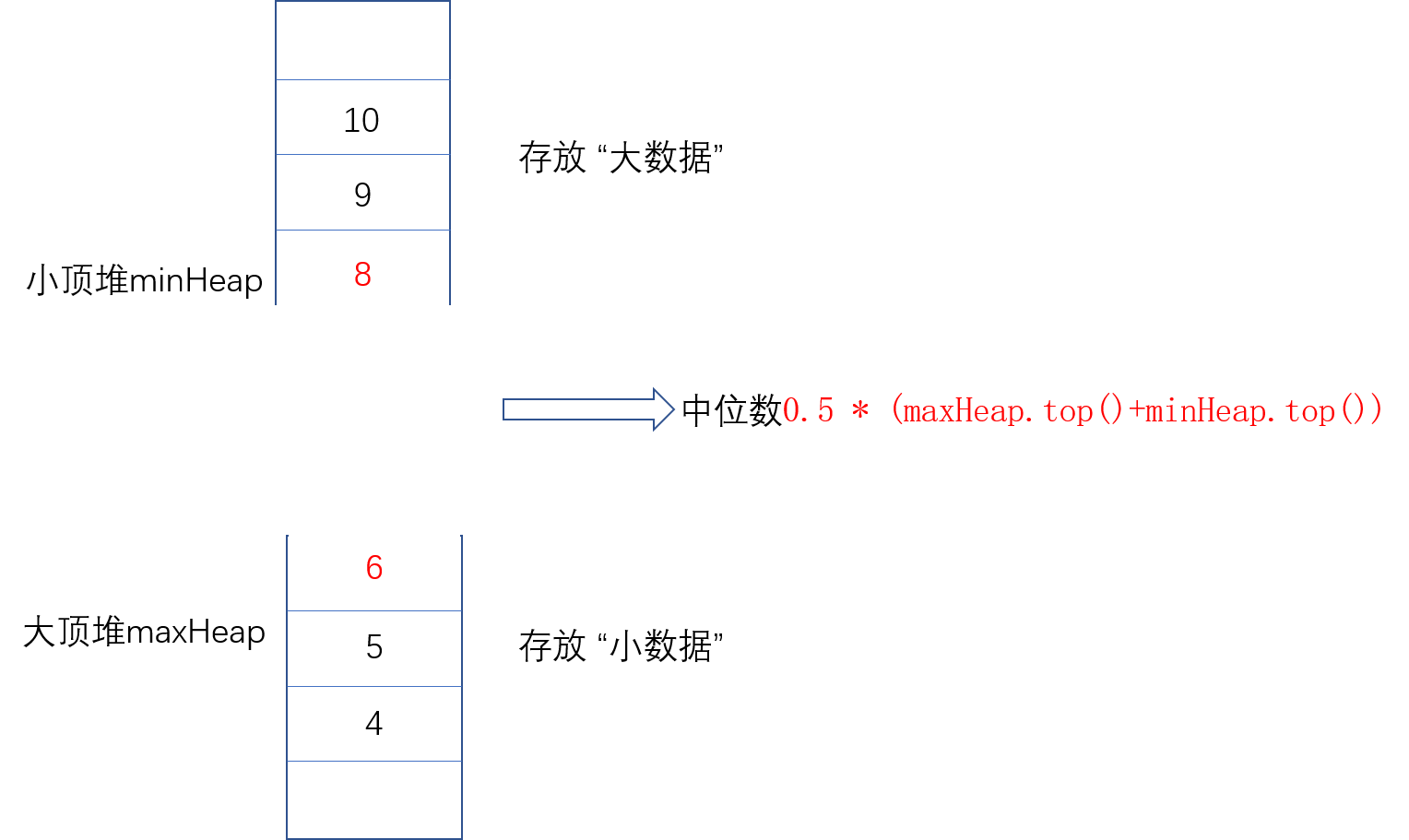
因为要求中位数,我们将数据分为两份,分别放在两个堆中。(利用堆顶具有该数据中最大或者最小值,也就是将整个数据流的分界线找到)
大数据堆:较大的数据,放在小顶堆(保证堆顶是大数据中最小值)
小数据堆:较小的数据,放在大顶堆(保证堆顶是小数据中最大值)
注意大数据堆和大顶堆的区别,大数据堆指的是存放两部分中较大的数据。上面看懂了可以忘掉大顶堆小顶堆,知道大数据堆和小数据堆即可,避免混淆
如何添加元素
1.当两个堆长度相等时,向大数据堆添加元素num(向小数据堆添加也可,同理)。添加时需注意得先向小数据堆添加num,由小数据堆重新得到堆顶最大值,将该值压入大数据堆。此举是为了保证新添加的元素先进入小数据堆,再由小数据堆选拔出最大值,送入大数据堆,保证两个堆顶依然是数据流的分界线。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sMizPHmC-1637656336026)(D:\桌面\添加元素举例.png)]
2.当两个堆长度不等时,也就是大数据堆长度大于小数据堆。向小数据堆添加元素。同理,先向大数据堆添加,由大数据堆选拔出最小元素送入小数据堆。保证两个堆顶依然是分界线。
如何获取中位数
1.当两个堆长度相等时。
1
return 0.5 * (maxHeap.top()+minHeap.top());
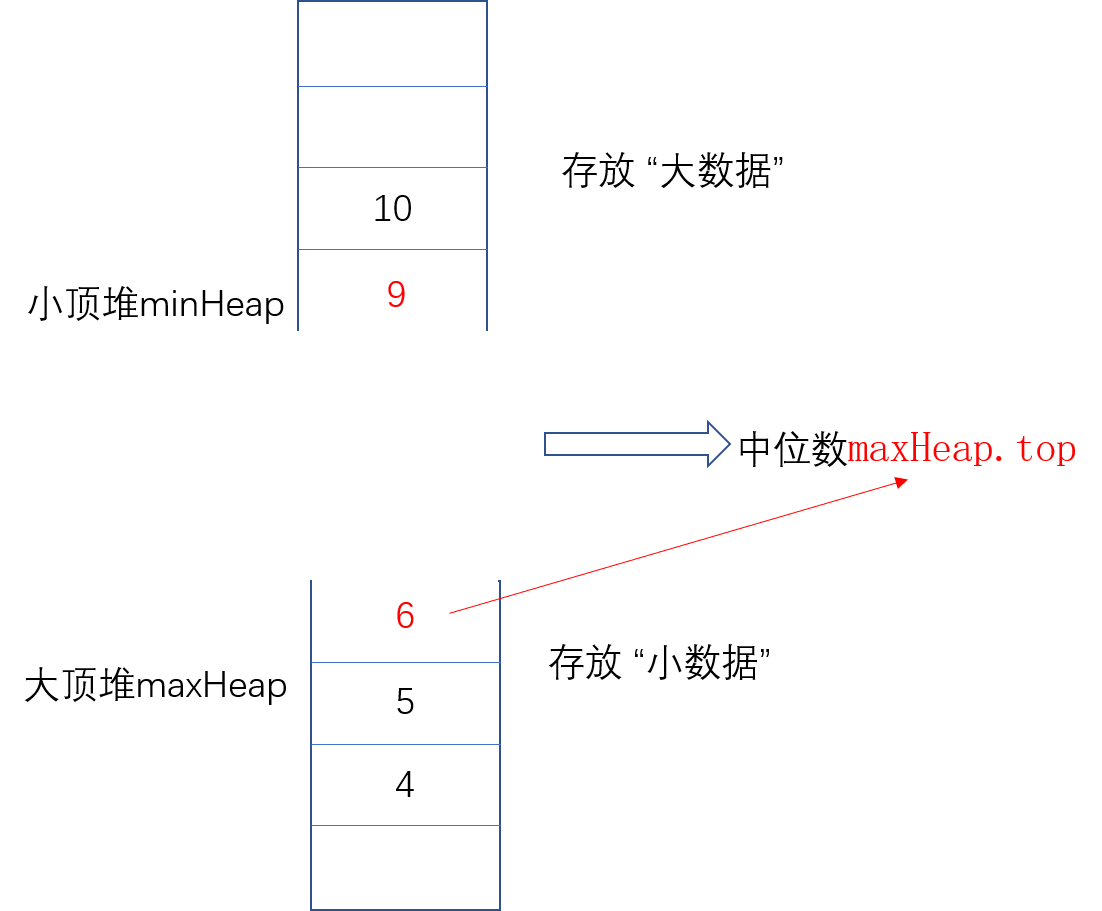
2.当两个堆长度不等时,也就是大数据堆长度大于小数据堆。
1
return maxHeap.top();
总结方法:
优先队列、堆排序
三、代码
1 | class MedianFinder { |



